A Teoria das Restrições, também denominada de TOC (Theory of Constraints) é um desenvolvimento relativamente recente no aspecto prático da tomada de diversas decisões organizacionais nas quais existem restrições. A TOC foi inicialmente descrita pelo Dr. Eliyahu Goldratt em seu livro, A Meta.
Uma restrição é qualquer coisa numa empresa que a impede ou limita seu movimento em direção aos seus objetivos. É claro que a aplicação da TOC requer uma apropriada definição dos objetivos a serem atingidos. Para a maior parte das empresas, o objetivo principal é o lucro presente e sua sustentabilidade no futuro. Existem dois tipos básicos de restrições: físicas e não-físicas. As restrições físicas na maior parte das vezes estão relacionadas a recursos: máquinas, equipamentos, veículos, instalações, sistemas etc. As restrições não-físicas podem ser a demanda por um produto, um procedimento corporativo ou mesmo um paradigma mental no encaminhamento de um problema.
Numa empresa industrial, a TOC envolve três indicadores de desempenho que permitem avaliar se o conjunto das operações está se movendo em direção aos objetivos (lucro):
- Rentabilidade: é a taxa pela qual a empresa constrói seu lucro através da comercialização de seus produtos. Em essência, a rentabilidade de um produto poderia ser aproximada pela margem de contribuição (preço de venda – custo variável das matérias-primas). Os custos de mão de obra e outros custos fixos são considerados como parte das despesas operacionais.
- Despesas operacionais: todo o dinheiro gasto pela empresa na conversão de seus estoques em margem de contribuição.
- Estoques: todo o dinheiro imobilizado pela empresa em coisas que podem ou poderiam ser comercializadas. Os estoques incluem não apenas os itens convencionais (matérias-primas, produtos em processamento e produtos acabados), mas também edifícios, terras, veículos, equipamentos. Não é incluído nos estoques, portanto, o valor do trabalho adicionado aos estoques dos produtos em processamento.
Percebe-se que a TOC possui uma ligação bastante forte com a contabilidade gerencial, especificamente com a abordagem de custeio pela margem de contribuição. Está claro que a utilização dos princípios geralmente aceitos na contabilidade financeira ou para fins legais pode levar a decisões subótimas, basicamente pela necessidade de alocar e ratear todos os custos fixos aos centros de custo, os quais, eventualmente, podem ser restrições. Outros quatro indicadores de desempenho podem ser calculados a partir da Rentabilidade, das Despesas operacionais e dos Estoques:
Margem líquida = rentabilidade – despesas operacionais
Retorno Sobre o Investimento (RSI) = (rentabilidade – despesas operacionais) / estoque
Produtividade = rentabilidade / despesas operacionais
Giro = rentabilidade / estoques
Deve ser observada a ligeira diferença destes indicadores, especificamente o Giro e o RSI, quando feita a transposição dos princípios da contabilidade financeira para a gerencial. Por exemplo, na contabilidade financeira, o Giro é definido como vendas / estoques.
Aplicação e Implementação
A TOC tem sido aplicada em três diferentes níveis de tomada de decisão: gerência da produção, na resolução de problemas relacionados aos gargalos, à programação e à redução dos estoques; análise de rentabilidade, levando à mudança de decisões baseadas em custo para decisões baseadas na melhoria contínua das operações que afetam a rentabilidade; e, gestão de processos, na identificação de fatores organizacionais, que não são necessariamente recursos, que impedem as empresas de atingirem seus objetivos.
São cinco os passos para aplicação da TOC.
- Identificar a restrição do sistema. Numa empresa industrial, a restrição pode ser o tempo disponível ou a capacidade de uma máquina, de um departamento ou de uma estação de trabalho. Para empresas de serviços ou de alta tecnologia, a restrição pode ser o tempo disponível dos funcionários mais capacitados.
- Calcular a rentabilidade por unidade de recurso consumida na restrição. Este valor é obtido pela divisão da rentabilidade ou margem de contribuição unitária pelo consumo de recursos da restrição para produzir um produto. A chave para maximizar o lucro é concentrar na produção e na comercialização de produtos com a maior rentabilidade por unidade de recurso consumida na restrição.
- Subordinar o sistema à restrição. Os recursos e estoques devem ser gerenciados de modo a prover exatamente o necessário para atingir os objetivos definidos para a restrição. Este passo pode implicar na ociosidade de recursos que não são restrições. Normalmente o sistema é subordinado a restrição através de um método de programação e controle da produção chamado de Tambor-Pumão-Corda (Drum-Buffer-Rope ou DBR).
- Romper ou elevar a restrição do sistema. Através da melhoria contínua das operações, da aquisição de capacidade ou de flutuações na demanda, por exemplo, a restrição do sistema pode ser rompida ou elevada, de modo que a esta restrição deixe de sê-lo. Uma nova restrição física ou não física, interna ou externa, assumirá o papel da restrição anterior.
- Identificar a nova restrição do sistema caso a restrição seja rompida.
Deve ser observado, no entanto, que a implementação da TOC pode exigir uma mudança substancial na maneira com que a empresa opera. Por exemplo, suponha que, numa empresa, produzir e comercializar o produto de menor preço unitário e maior demanda maximize o lucro (objetivo). Se a empresa remunera sua força de vendas com base em comissões como um percentual da receita, pode existir um incentivo implícito para vender os produtos mais caros. Este cenário demandaria uma nova política de remuneração da força de vendas.
Tambor-Pumão-Corda (DBR)
O DBR é o método de programação e controle da produção que permite subordinar o sistema à restrição. Seu objetivo é assegurar a máxima utilização da restrição para atender à demanda. O Tambor (Drum) é a programação detalhada da restrição, com os itens a ser produzidos, suas quantidades, os horários de início e de término. A demanda é o ponto de partida para a determinação do Tambor.
Os recursos que não são restrição devem seguir o ritmo da restrição. É por isto que a programação da restrição é chamada de Tambor, por “determinar o ritmo de toda a tropa”. Os recursos que não são restrição devem ser gerenciados de modo a não faltarem itens na restrição, caso contrário, o objetivo será ameaçado. Como os recursos que não são restrição possuem maior capacidade que a demanda, não é necessário programá-los. O método DBR sinaliza para a liberação dos itens necessários para a alimentação do Tambor e para que os recursos que não são restrição processem esta quantidade o mais rápido possível.
Em função das incertezas, uma proteção deve ser criada para a liberação dos itens algum tempo antes de seu processamento na restrição. Esta proteção é chamada de Pulmão (Buffer), e na TOC, o Pulmão é medido em unidades de tempo, e não quantidades de itens. A duração do Pulmão é influenciada pela velocidade dos outros recursos que não são restrições e pela variância do tempo de resposta das operações. Maior a variância, maior a duração do Pulmão. Maior a velocidade dos outros recursos, menor o Pulmão.
Em linhas gerais o Pulmão é criado para proteger a programação. É uma antecipação do instante de liberação dos itens de modo a garantir o cumprimento do programa de produção. Na TOC pode haver três tipos de pulmão:
- Pulmão da Restrição (Constraint Buffer) – objetiva proteger o Tambor com a liberação antecipada dos itens para a restrição.
- Pulmão do Carregamento (Shipping Buffer) – a restrição não é o único elemento com programas a serem observados. O carregamento dos produtos acabados também deve ser protegido com um pulmão, de modo a ser assegurada a confiabilidade dos prazos para os clientes.
- Pulmão da Montagem (Assembly Buffer) – quando os itens que foram processados pela restrição devem ser montados com itens que não passaram pela restrição, é necessário criar outra proteção. Neste caso, todas as partes que passaram pela restrição devem ser utilizadas para formar o produto acabado e desta forma, nenhum item “não-restrição” deve estar faltando.
Nem todas as empresas industriais necessitam dos três tipos de pulmão. Esta decisão depende do tipo de processo e da localização da restrição. Se existe uma restrição física, associada a um recurso, haverá pelo menos 2 pulmões, o da restrição e o do carregamento. O Pulmão da Montagem será necessário se houver uma operação que conjuga itens que foram com outros que não foram processados por restrições. Todos os itens se enquadram em duas alternativas:
- Os itens que são processados pela restrição terão em seu fluxo dois pulmões: da Restrição e do Embarque.
- Os itens que são montados com outros itens que são processados pela restrição terão em seu fluxo dois pulmões: da Montagem e do Embarque.
Tomando o Tambor como o ponto de partida e subtraindo o Pulmão da Restrição é possível determinar o instante da liberação dos itens. A Corda assegura que será liberada a quantidade exata de itens que será processada pela restrição. Em outras palavras, através da Corda é assegurado que todos os recursos operarão no mesmo ritmo que a restrição, sem elevação nos níveis de estoque em processamento.
A aplicação do método DBR para subordinação do sistema à restrição, deve observar outros passos adicionais, além dos cinco passos comentados na seção anterior:
- Representar num gráfico de Gantt o Tambor, ou seja, a programação detalhada da restrição ao longo do tempo;
- Decidir o tamanho adequado dos pulmões de Restrição, de Montagem e de Carregamento para cada produto;
- Subtrair o Pulmão da Restrição do início da operação da correspondente restrição, representada no gráfico de Gantt, para determinar o instante de liberação dos itens de modo a apoiar o Tambor.
- Subtrair o Pulmão da Montagem do final da operação da correspondente restrição para determinar a liberação dos itens de modo a apoiar a montagem de itens que não foram processados pela restrição com itens que foram processados pela restrição.
- Adicionar o Pulmão do Carregamento ao final da operação da correspondente restrição para determinar a data de carregamento do produto, se a produção for para estoque. Se a produção for contra-pedido, o Pulmão do Carregamento deve ser subtraído da data de entrega para determinação do instante de liberação dos itens.
- Desenvolver uma programação para a produção de itens em pontos divergentes, ou seja, uma operação onde dois ou mais produtos podem ser fabricados a partir do mesmo item em comum com base nas programações da restrição, do carregamento e da montagem.
Na seção seguinte é exemplificada a adoção dos passos da TOC e do método DBR numa empresa fictícia que fabrica dois produtos.
Aplicação Prática
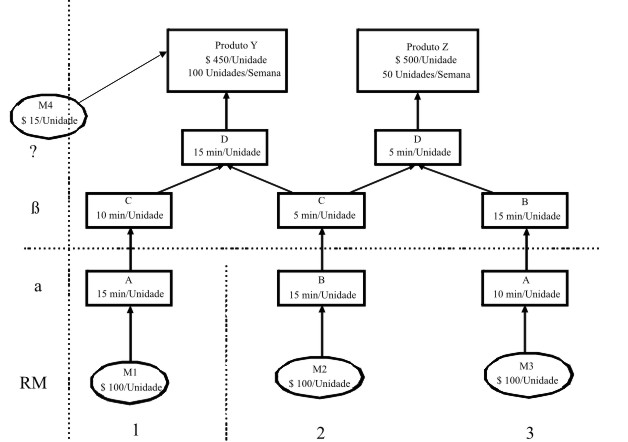
Uma empresa fabrica dois produtos, Y e Z que são processados em quatro departamentos, A, B, C e D. O produto Y requer três tipos de materiais: M1, M2 e M4. O produto Z requer dois tipos de materiais, M2 e M3. Na Figura 1 são representadas as lógicas das estruturas dos produtos (logical product structures). A combinação da lista de materiais ou itens (bill of materials) de um produto com o roteiro das operações (ou das estações de trabalho, ou dos departamentos) percorrido pelos itens que compõem este produto (part routings) forma a lógica da estrutura dos produtos.
Os requisitos de fabricação para cada produto são resumidos na Tabela 1:
|
|||||||||||||||||||||||||||
| Tabela 1 – Consumo de recursos e de capacidade por produto |
Cada departamento tem 2400 minutos de capacidade disponível por semana. As despesas operacionais desta empresa hipotética são de $ 30000 por semana. Com base na demanda corrente, a empresa consegue vender 100 unidades do produto Y e 50 unidades do produto Z por semana. Os preços de venda são $ 450 para o produto Y e $ 500 para o produto Z. Todos os quatro materiais são disponíveis em quantidades suficientes. A mão de obra necessária também está disponível.
A abordagem que é apresentada a seguir é particularmente útil quando são apenas dois produtos e existe apenas uma restrição ativa além da demanda. Todavia, a abordagem por programação linear torna-se necessária em situações mais complexas, com múltiplos produtos e diversas restrições ativas além da demanda.
O primeiro passo consiste na determinação da restrição do sistema. Para isto, as necessidades totais de tempo de cada departamento para se atender a demanda semanal corrente de Y e de Z devem ser calculadas, conforme é indicado na Tabela 2, e confrontadas com a capacidade disponível.
|
||||||||||||||||||||
| Tabela 2 – Consumo da capacidade pela demanda semanal |
Como cada departamento possui capacidade disponível de 2400 minutos por semana, o departamento B é a restrição por não possuir capacidade suficiente para atender semanalmente às 100 unidades de Y e às 50 unidades de Z.
O segundo passo depende inicialmente da determinação da rentabilidade ou da margem de contribuição unitária para cada produto. Isto é necessário para determinar como gerenciar a restrição de modo a maximizar o lucro. A rentabilidade unitária é dada na Tabela 3.
|
|||||||||
| Tabela 3 – Cálculo da margem de contribuição unitária por produto |
Na Tabela 3 são fornecidos os elementos necessários para completar o segundo passo e determinar a rentabilidade por unidade de recurso consumida na restrição para fabricar o produto. Este cálculo é indicado na Tabela 4.
|
|||||||||
| Tabela 4 – Rentabilidade unitária por unidade de recurso consumida |
O terceiro passo consiste na subordinação do sistema à restrição. Nesta aplicação prática, a maximização do lucro passa pela fabricação do maior número possível de unidades com maior rentabilidade por unidade de recurso consumida na restrição. Para atender a demanda, a empresa deveria produzir 100 unidades de Y. Isto consumiria (100 unidades)(15 minutos) = 1500 minutos da capacidade disponível de B e deixaria 2400 – 1500 = 900 minutos semanais para a fabricação de 30 unidades de Z, ou seja, 900 minutos / 30 minutos por unidade = 30 unidades.
Na Figura 2 é ilustrada graficamente a abordagem adotada para determinação dos tamanhos de lote de produção. Para construir este gráfico, devem ser determinadas inicialmente as restrições que delimitam o espaço das soluções viáveis. Nesta empresa, as restrições são a demanda corrente pelos dois produtos (Y = 100 e Z = 50) e o trade-off do consumo de recursos do departamento B por unidade produzida (15Y + 30Z = 2400). Observando-se este trade-off e ignorando-se as demandas correntes, o departamento B poderia produzir 160 unidades de Y (2400/15) e nenhuma unidade de Z ou 80 unidades de Z (2400/30) e nenhuma de Y ou qualquer combinação de Y e Z que totalize 2400 minutos semanais. Esta combinação é representada pela linha que liga estes pontos na Figura 2.
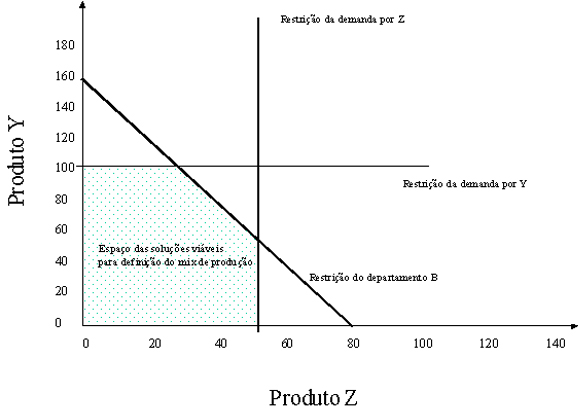 |
| Figura 2 – Representação gráfica das restrições |
A solução que maximiza a margem de contribuição deve ser encontrada nos vértices que delimitam o espaço das soluções viáveis.A margem de contribuição é dada pela equação 235Y + 300Z. Na Tabela 5 são apresentados os resultados para a equação da margem de contribuição em função destes vértices.
|
||||||||||
| Tabela 5 – Teste dos vértices do espaço de soluções viáveis |
Finalmente, o lucro semanal pode ser calculado ao serem incorporadas as despesas operacionais. Lucro semanal = $ 32500 – 30000 = $ 2500. Uma vez que a restrição foi identificada e o mix de produção definido, um gráfico de Gantt detalhando o Tambor (programação da restrição, ou seja, do departamento B) deve ser construído. Diversas programações são viáveis e, para efeito de simplificação, supõe-se que não há incertezas no sistema e que o cliente não estabeleceu prazos para recebimento, de forma que todos os pulmões (restrição, montagem e carregamento) são iguais a zero. Também supondo os tempos de set up iguais a zero no departamento B, lotes iguais à demanda diária podem ser produzidos sem a criação de uma nova restrição. Neste caso, seriam 20 unidades de Y (100/5) e 6 unidades de Z (30/5) para turnos de 480 minutos (2400/5). O gráfico de Gantt para o Tambor é apresentado na Figura 3, além dos instantes para liberação e recebimento dos itens nas operações realizadas em cada departamento. Percebe-se que a taxa de utilização da restrição é de 100%, ao passo que a utilização nos outros departamentos é inferior ao limite máximo, sendo alternados períodos de ociosidade com ocupação.
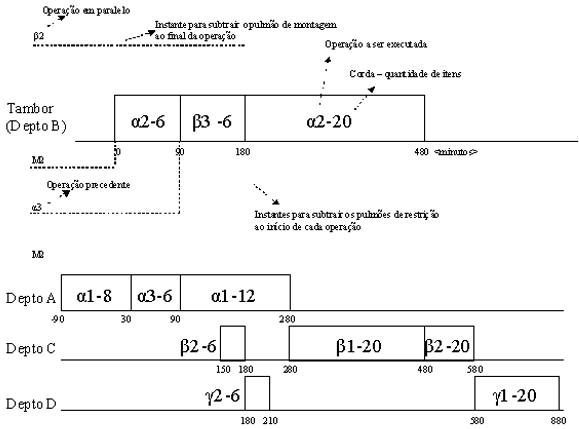 |
| Figura 3 – Possível programa de produção para um turno do Tambor |
CONCLUSÃO
A TOC é uma filosofia para o planejamento da produção, ancorada em técnicas de programação linear, na qual as restrições determinariam o desempenho (lucratividade) do sistema. A operacionalização do planejamento pela TOC em um programa de produção ocorre através do método DBR. Pelo DBR, todo o sistema é subordinado à programação da restrição (Tambor), os diferentes pulmões são incorporados para proteger o tambor das incertezas do sistema e as cordas asseguram a liberação das quantidades exatas.
O objeto de análise pela TOC e pelo DBR é a lógica da estrutura dos produtos, ou seja, a combinação da lista de materiais com o roteiro das operações (ou das estações de trabalho) percorridas pelos itens que compõem estes produtos. No MRP (Materials Requirements Planning), ao contrário, o objeto de análise para formulação do planejamento e da programação da produção é a lista de materiais e sua defasagem no tempo, de modo a assegurar a execução do MPS (Programa Mestre de Produção) a partir de uma previsão de vendas.
Dado que não é possível afirmar, a priori, a superioridade da TOC sobre o MRP ou qualquer outra política para o planejamento e a programação da produção, a escolha de uma determinada política depende substancialmente de quão fácil e direta é a associação entre matérias-primas, itens em processamento e necessidades líquidas com a programação de produtos acabados. Silver, Pike e Peterson defendem que existe uma conexão direta entre a posição na matriz produto-processo e a facilidade desta associação. Neste caso, conforme ilustra a Figura 4, a TOC seria, por exemplo, mais adequada para situações job shop (oficina) com diversos produtos principais.
BIBLIOGRAFIA
Anônimo, “What is the theory of constraints and how does it compare to lean thinking?” in www.qmi.ans.au (acesso em 17/12/2003).
Corbett, T., 2003, “Drum-Buffer-Rope” in www.corbett.pro.br (acesso em 17/12/2003).
Silver, E., Pyke, D., Peterson, R., 2002, Inventory Management and Production Planning and Scheduling, 3rd Edition, New York: Wiley & Sons.
Sytsma, S., 2003, “The Theory of Constraints – Making Process Decisions Under Conditions of Limited Resources, Capacities or Demand” in www.sytsma.com.