A divergência de metas entre as variadas áreas organizacionais é um tema de constante conflito no mundo empresarial. Apesar dos grandes esforços despendidos durante os planejamentos estratégicos ao final de cada ano, sempre fica a impressão de que as metas entre departamentos sob diferentes diretorias entram em conflito. E o que se observa recai sobre o conceito da falácia da composição, onde o empenho pelo cumprimento das metas individuais não leva ao máximo global.
É bastante comum vermos, por exemplo, as áreas comerciais e de finanças em conflito: enquanto que o comercial possui uma meta clara para atração de clientes, podendo ser alcançada através de prazos mais generosos de recebimento, a área de finanças quer reduzir o capital de giro. Isso gera um conflito de interesses, e é praticamente impossível que ambas as metas sejam cumpridas, quiçá o objetivo global da empresa. Um outro caso hipotético envolvendo conflito de metas: a área de compras, com o objetivo de reduzir custos unitários, decide comprar em volumes maiores, causando um aumento nos custos relacionados a estoques, o que iria de encontro às metas de redução de custos da área Logística. Enfim, são muitos exemplos que ilustram os conflitos internos existentes nas empresas.
A melhor definição de um planejamento estratégico é tarefa árdua e gera uma série de dificuldades, mas como em qualquer realidade empresarial, tais problemas precisam ser encarados e resolvidos. E dentre as ferramentas que existem hoje para resolução de conflitos, destacamos a Teoria dos Jogos.
O filme “Uma Mente Brilhante”, vencedor do Oscar de melhor filme em 2001, retrata a história de um dos maiores matemáticos de todos os tempos, o americano John Nash. Apesar da atuação brilhante de Russel Crowe enfatizando a dificultosa vida do matemático para lidar com sua genialidade e com sua esquizofrenia, o filme peca por alterar de maneira substancial a biografia do matemático por motivos comerciais, deixando um pouco de lado o brilhantismo acadêmico e a fenomenal contribuição que John Nash deixou para a matemática, economia e outros campos da ciência.
A Teoria dos Jogos lida, basicamente, com interações estratégicas de jogadores. A intenção deste post é apresentar, de maneira simples e prática, como alguns de seus conceitos podem servir para aplicações básicas de resoluções de conflitos entre dois jogadores. Primeiramente, devemos entender como funciona a Matriz de Ganhos em um Jogo, do que se trata as Estratégias Dominantes e o Equilíbrio de Nash e entender também o clássico Dilema do Prisioneiro.
A Matriz de Ganhos é uma forma de abordagem simples que permite visualizar como a interação da escolha de dois agentes afeta nos resultados obtidos por cada um deles. Vejamos num exemplo: Num jogo em que duas pessoas, chamadas aqui de A e B, podem escolher duas estratégias diferentes – A escolhe entre alto ou baixo e B escolhe entre esquerda e direita – a Matriz de Ganhos permite a visualização dos ganhos obtidos por cada pessoa, como uma matriz: o primeiro número se refere ao ganho de A e o segundo ao ganho de B.
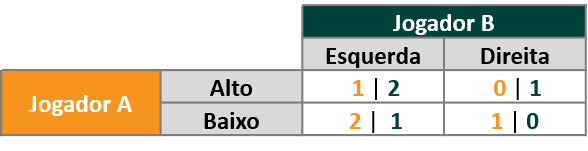
Figura 1 – Exemplo de Matriz de Ganhos
Fonte:ILOS
Neste jogo podemos observar que existe, para cada jogador, de maneira isolada, uma melhor estratégia: Para A sempre será melhor escolher “baixo”, e para o jogador B sempre será melhor escolher “esquerda”. Neste caso, o resultado natural seria baixo e esquerda, resultando num ganho 2 para o jogador A e 1 para o jogador B. Teríamos aqui uma Estratégia Dominante, pois há uma escolha ótima para cada jogador qualquer que seja a escolha do outro.
No entanto, para a tristeza dos tomadores de decisões estratégicas, o que se observa é que a estratégia dominante não ocorre com tanta frequência. Normalmente a escolha dos jogadores afeta a escolha do outro, de forma que é impossível prever o resultado sem saber previamente suas escolhas. Em contrapartida à forte exigência da estratégia dominante, de que a escolha de A seja ótima para todas as escolhas de B, poderíamos ter escolhas ótimas para A dada a escolha de B. Isto configura o Equilíbrio de Nash, que define jogos em que existe uma escolha ótima de A dada a escolha de B e uma escolha ótima de B dada a escolha de A.
Um exemplo de jogo em que se observa a existência de uma estratégia dominante é o clássico Dilema do Prisioneiro: Dois prisioneiros, parceiros num crime, são interrogados em locais separados. Cada um tem duas escolhas possíveis: de confessar o crime e envolver a participação do comparsa ou negar sua participação, permanecendo em silêncio. Se ambos confessassem a participação do outro comparsa, receberiam, cada um, uma pena de 3 anos de prisão. Se somente um confessasse a participação do outro e esse outro negasse, a pena daquele que negou seria de 6 anos, enquanto que aquele que testemunhou seria solto, como benefício pelo auxílio na resolução do caso. Se ambos negassem, cada um ficaria preso por 1 ano. A figura 2 apresenta a matriz de ganhos do Dilema do Prisioneiro. Note que o número negativo representa uma perda, portanto, neste caso, quanto menor a perda, melhor.

Figura 2 – Matriz de Ganhos no Dilema do Prisioneiro
Fonte:ILOS
Neste jogo, podemos observar que existe uma estratégia dominante: Qualquer que seja a escolha de B (confessar ou negar), o prisioneiro A estará melhor se confessar, e vice-versa. Desta forma, a estratégia dominante levaria a situação em que ambos confessariam, cumprindo cada um uma sentença de 3 anos. No entanto, se ambos se mantivessem calados e negassem o crime, os dois melhorariam, obtendo somente 1 ano de reclusão cada. Então a questão que fica é: como coordenar a escolha de ambos, de maneira que a estratégia de negar seja escolhida pelas duas partes? Em que situação eles deveriam confiar um no outro?
O que se observa é que se o jogo ocorresse uma única vez, confessar parece razoável. Lembre-se que se o jogador burla (confessa), ele pode ter o benefício de sair imediatamente da prisão, caso o outro negue a participação. Mas se este jogo se repetir inúmeras vezes, confessar seria a melhor estratégia?
Quando estamos em um caso de jogos repetitivos, o racional e mais eficiente é escolher uma estratégia cooperativa, de maneira coordenada. Em uma série de experimentos liderados por Robert Axelrod, testados em um torneio computacional, foi comprovada que em jogos onde sempre existe a perspectiva de uma nova rodada futura (ou seja, um jogo com infinitas repetições sequenciais), a melhor estratégia é a chamada “olho-por-olho”: o jogador tenta sempre cooperar, até que seu adversário burle a cooperação. Caso isso aconteça, o jogador “pune” seu adversário burlando na jogada seguinte, e continuará burlando até que seu adversário decida voltar a cooperar, levando ao retorno do movimento de cooperação do jogador na jogada seguinte. Ou seja, o jogador sempre buscará a cooperação, punindo quando seu adversário burla e perdoando seu adversário quando ele coopera.
Se imaginarmos diferentes departamentos como “jogadores” e tentarmos aplicar a Matriz de Ganhos da Teoria dos Jogos para definição do melhor ganho em termos de metas, estaríamos numa situação de jogos repetitivos: visto que ano após ano aqueles mesmos departamentos coexistirão e precisarão “jogar” novamente para decidir suas metas, a estratégia da cooperação deveria ser escolhida por ambos. Apesar de parecer uma conclusão óbvia, ela não é tão fácil de ser aplicada, visto que existe uma enorme dificuldade para definição dos ganhos dos jogadores para definição da Matriz.
A ferramenta da Teoria dos Jogos é poderosa, e sua aplicação ainda se restringe bastante às áreas financeiras. Porém seus conceitos podem ser utilizados nas mais diversas situações, onde exista conflito e a negociação entre as partes seja inevitável. Fica uma provocação no ar: Onde mais poderíamos aplicar tais conceitos no âmbito empresarial? Em que áreas ao longo da cadeia de suprimentos, permeadas de decisões estratégicas, poderíamos utilizar tal ferramenta?
Referências:
VARIAN, Hal R. Microeconomia-princípios básicos. Elsevier Brasil, 2006.
AXELROD, Robert M. The evolution of cooperation. Basic books, 2006.
