Conforme foi apontado na primeira parte deste artigo1, a gestão estratégica de estoques vem ganhando importância cada vez maior na gestão da cadeia de suprimentos. Pesquisa realizada pelo ILOS2 revela a importância de custos com estoque para empresas brasileiras. Dos custos logísticos totais, os estoques constituem uma parcela de 26%, porcentagem menor apenas do que os gastos com transportes.
A mesma pesquisa revela, ainda, que os custos logísticos representam 11,6% do Produto Interno Bruto nacional, dos quais 3,5% são relativos aos estoques.
Especificamente, as decisões principais a serem tomadas no gerenciamento de estoques – quanto pedir, quando pedir, quanto manter em estoque de segurança, onde localizar os estoques e como controlar o sistema – podem ser auxiliadas pela aplicação dos conceitos de mapa de estoque.
A partir desses conceitos, foram desenvolvidas ferramentas de uso simples, em Ms Excel/VBA, para auxiliar o tomador de decisão. Essas ferramentas serão discutidas nesta parte do artigo. Além disso, foi feito um estudo de caso para uma empresa do setor de agronegócio.
SISTEMAS DE APOIO À DECISÃO
Buscando maior facilidade na gestão de estoques, foram desenvolvidas três ferramentas de uso simples, em Ms Excel, para apoiar a tomada de decisão.
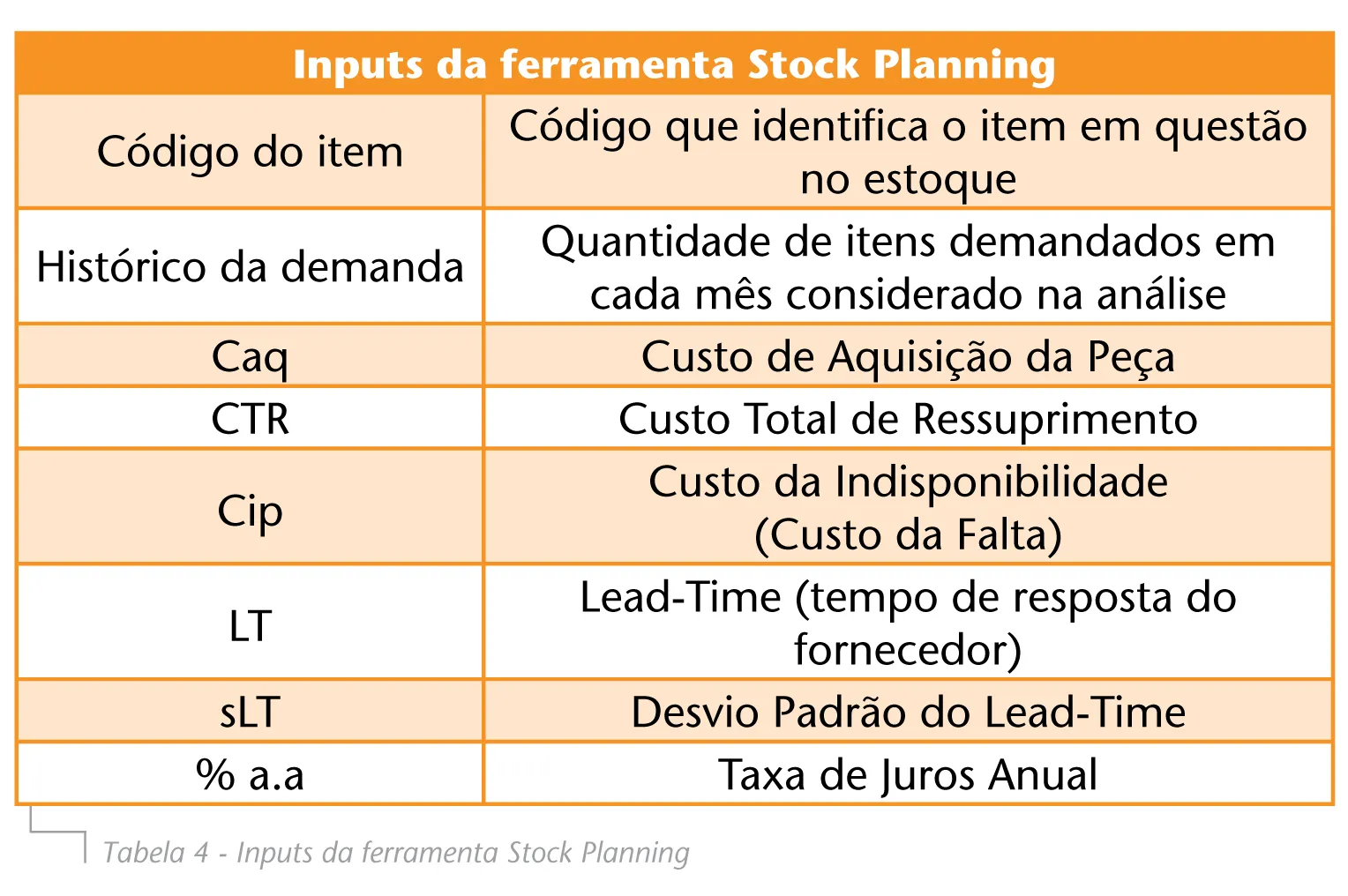
A primeira delas, a ferramenta Stock Planning, tem como objetivo planejar a quantidade de estoque de peças de reposição necessária para atender a um nível de serviço desejado pelo tomador de decisão. Após a inserção dos dados na planilha, as peças de reposição são classificadas em peças de baixíssimo giro, baixo giro e alto giro, conforme explicitado na seção 2. Os inputs da ferramenta são mostrados na Tabela 4.
A ferramenta apresenta como outputs o nível de estoque e o investimento necessário para manutenção dessa quantidade em estoque, bem como o custo de oportunidade associado. Isso é feito para três níveis de serviço: 90%, 95% e 98% no caso das peças de consumo de massa e de baixo giro.
Cabe notar que, para os itens de baixíssimo giro, os outputs mencionados são calculados apenas quando se opta pela manutenção dos itens em estoque. Essa decisão é tomada a partir da comparação entre os custos CT(0) e CT(1), também calculados pela planilha.
A segunda ferramenta
– Lumpy Demand – é uma alternativa à ferramenta Stock Planning para a gestão de peças de baixo giro com demanda oscilante, cujo objetivo principal é o cálculo do ponto de pedido.
Os inputs são: código do item, histórico da demanda e lead-time. Como outputs, são fornecidos o nível de estoque (lote Q), a fração de falta e o ponto de pedido, além dos parâmetros da distribuição Stuttering Poisson3.
O uso da distribuição Stuttering Poisson é uma alternativa para itens erráticos. É resultado da combinação das distribuições geométrica e Poisson. Isso acontece quando a chegada de pedidos é representada por λ (parâmetro da Poisson) e o tamanho do lote pedido é representado por ρ
(parâmetro da geométrica).
Através do uso dessa distribuição, probabilidades tabeladas permitem a determinação do ponto de pedido por meio de regressão linear.
É importante ressaltar que o uso da Lumpy Demand só pode ser feito quando a principal restrição é atendida – a quantidade média pedida deve ser positiva e inferior a um (0≤ρ≤1). Caso contrário, a ferramenta Stock Planning deverá ser usada. A classificação dos itens, bem como o mapa de estoque, foram apresentados na seção 2.4.
A terceira ferramenta foi desenvolvida com base na dissertação de mestrado de Silva (2009). Assim como a Lumpy Demand, esta ferramenta é uma alternativa para os itens de baixo giro, que apresentam grande variabilidade nos padrões da demanda. É baseada na demanda durante o lead-time.
O autor assume a aderência da demanda durante o lead-time (DLT) às distribuições La Place e Gama. A primeira não é somente indicada para itens slow-moving, mas uma alternativa à Normal para itens fast-moving quando há mais propagação nas caudas, se distanciando do perfil da distribuição Normal (Silva, 2009). O uso da distribuição Gama é sugerido por Silver, Pyke e Peterson (1998) em situações nas quais a distribuição da demanda é inclinada para a direita ou quando o coeficiente de variação (σL/DL) é superior a 0,5.
O diferencial dessa ferramenta está na metodologia usada para estimar a demanda durante o lead-time (LTD). Dados são gerados pelo método bootstrap modificado, apresentado por Willemain, Smart e Schwarz (2004), conforme cita Silva (2009). Nesse método, é gerada uma sequência de valores nulos e não nulos para todo o horizonte de previsão.
Os inputs da terceira ferramenta são os mesmos utilizados pela Stock Planning e apresentados na Tabela 5, com exceção da taxa de juros anual. Como outputs são fornecidos o ponto de pedido, o lote Q e a taxa de fi ll-rate, além do custo total de estoque.
APLICAÇÃO DAS FERRAMENTAS
Motivado pela importância estratégica da gestão de estoques, foi feito um estudo de caso para uma fabricante de equipamentos para o setor agrícola que mantém mais de 20 mil peças estocadas.
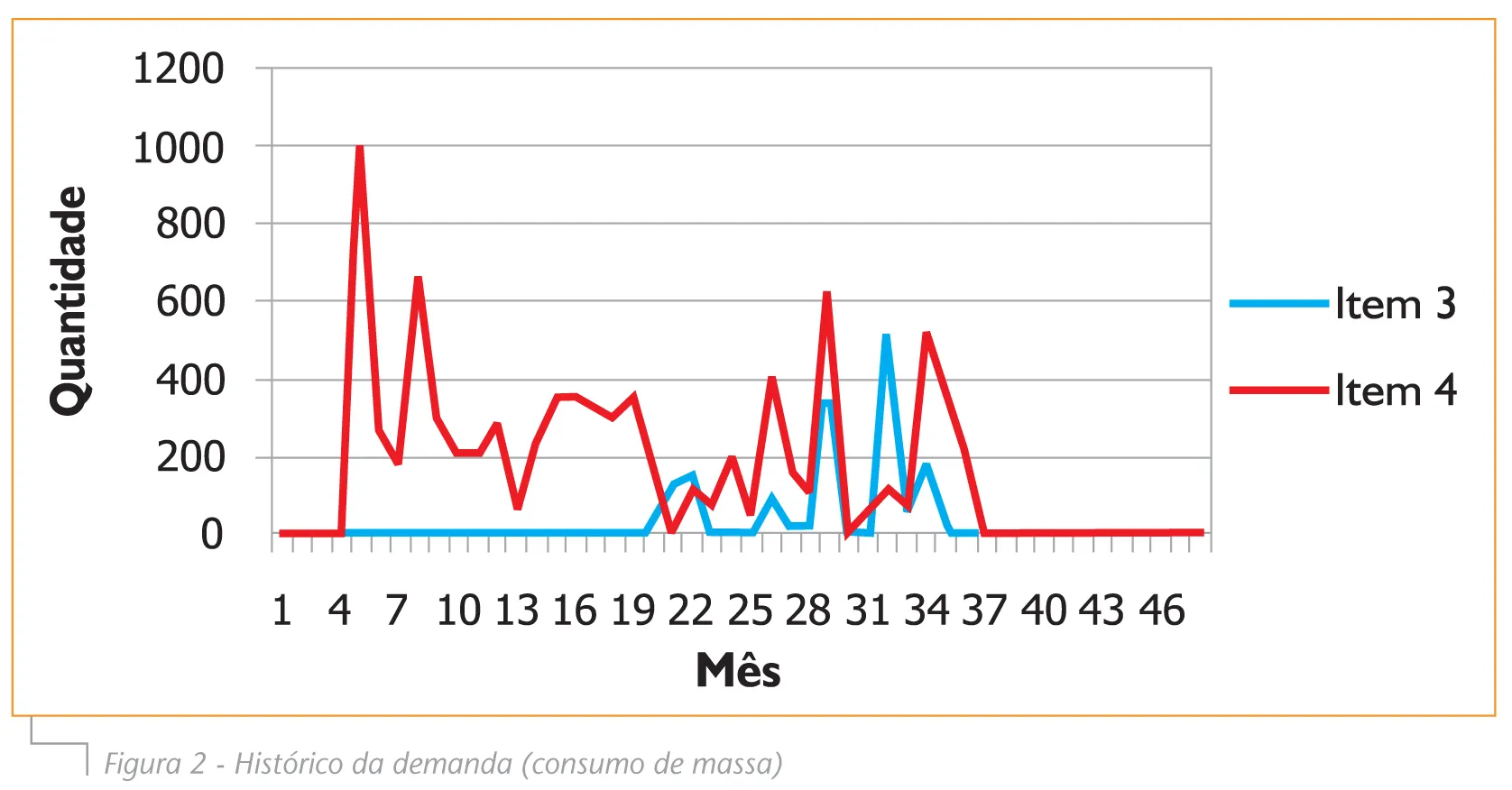
Para ilustrar o uso das ferramentas descritas na seção anterior, utilizamos séries de seis itens com características diferentes. Primeiramente, foi usada a ferramenta Stock Planning, que forneceu uma primeira classificação dos itens, como pode ser visto na Tabela 5. Cabe destacar que o item 2, de baixo giro, foi considerado com demanda aderente à distribuição Gama, e não à Poisson.
Para garantir um nível de serviço de 90%, devem ser mantidas 303 unidades do item 3 e 432 do item 4, totalizando 735 unidades em estoque. Para elevar o nível de serviço a 95%, 1.598 unidades devem ser estocadas, aumentando o investimento em estoque e o custo de oportunidade em 57%. Se o nível de serviço desejado for 98%, a quantidade de itens estocados salta para 2.946 unidades, aumentando em 77% o custo de oportunidade e o investimento em estoque, com relação a 90% de nível de serviço.
O estoque para o item de baixo giro (item 2) deve ser igual a 490 unidades para o menor nível de serviço considerado. Elevando-se este em 5 p. p., o aumento do estoque deve ser de 26%, enquanto o investimento cresce em 59%.
O uso da primeira ferramenta nos permite concluir, ainda, que os itens de baixíssimo giro (1, 5 e 6) devem ser estocados, uma vez que, nas três situações, obtivemos CT(0) > CT(1).
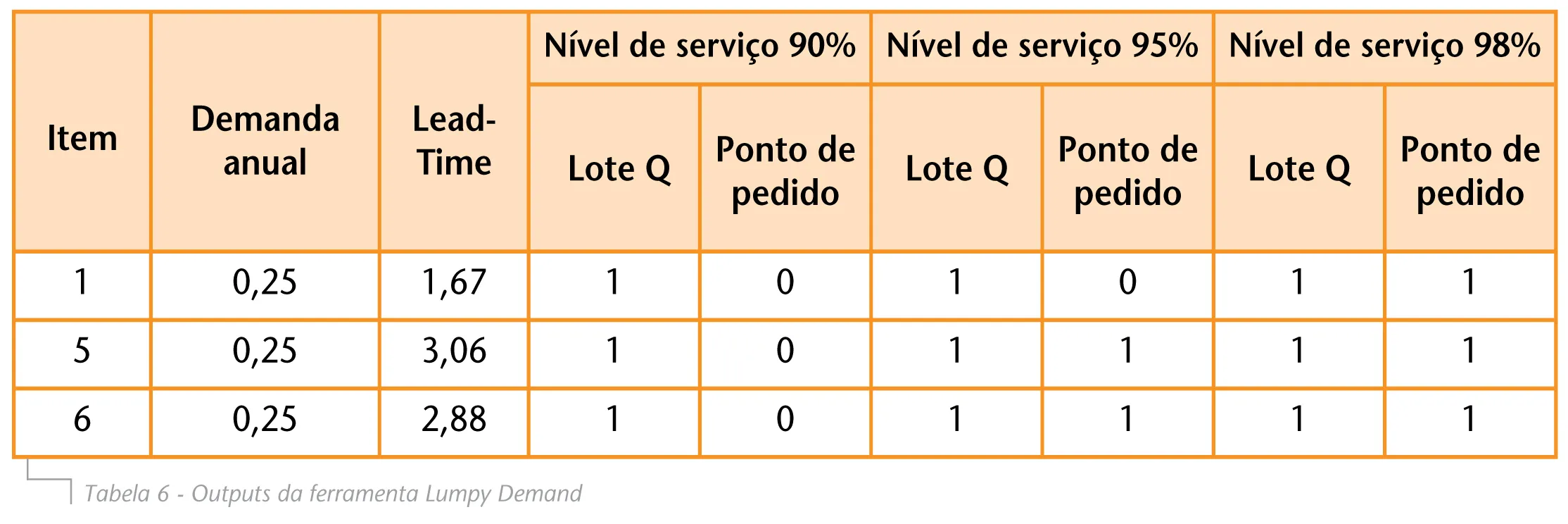
A ferramenta Lumpy Demand fornece o tamanho do lote, que no caso dessas três peças deve ser igual a um para os diferentes níveis de serviço analisados. A Tabela 3 compara os pontos de pedido para os itens 1, 5 e 6, além de mostrar a demanda média anual e o lead-time de ressuprimento.
Podemos notar que o ponto de pedido varia de zero, ao menor nível de serviço, até um, ao maior nível para todos os itens. Apenas ao nível de serviço de 95% os pontos de pedidos diferem. Nota-se que, embora os itens tenham a mesma demanda média anual e, consequentemente, os mesmos parâmetros para distribuição Stuttering Poisson, os pontos de pedido diferem. Essa diferença é dada pela variação no lead-time.
O uso da terceira ferramenta nos leva a outra classificação dos itens, conforme a Tabela 4.
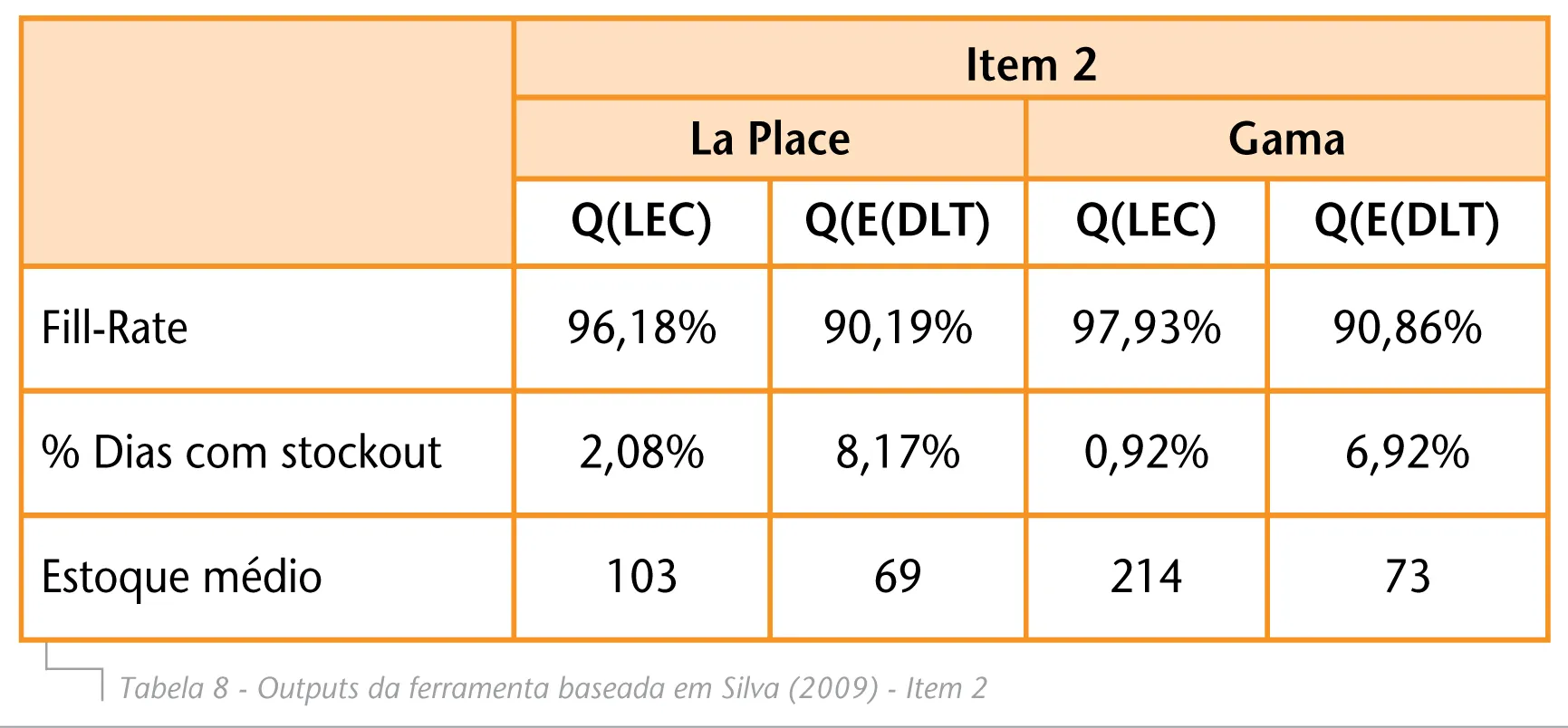
Considerando uma probabilidade desejada de não haver falta de 10%, a ferramenta indica que, para o lote econômico Q(LEC), o estoque médio é igual a 103 unidades, garantindo uma taxa de fill-rate igual a 96,18% e 2,08% de dias com stockout, quando usada a distribuição La Place. A distribuição Gama aponta que o lote econômico é de 214 unidades, com fill-rate de 97,93% e a porcentagem de dias com stockout de 0,92%. Para este item, portanto, pode-se dizer que a distribuição Gama é uma aproximação melhor para o item 2.
Como diferencial desta ferramenta, é possível calcular também o lote Q da demanda durante o lead-time.
A distribuição La Place aponta um estoque médio de 69 unidades, com fill-rate de 90,19%, enquanto a distribuição Gama nos fornece fill-rate de 90,86% e lote de 73 unidades.
Conclusão
O presente artigo atenta para a importância da implantação de políticas de controle de estoque nas empresas, as quais gerenciam uma quantidade cada vez maior de SKUs. Se, por um lado, esta variedade torna a gestão de estoques mais complexa, por outro desponta como diferencial competitivo, fundamental nos dias de hoje.
O uso das ferramentas desenvolvidas em Excel/VBA pode ser uma alternativa simples para os gestores, uma vez que permite simular os custos totais de estoque para diferentes níveis de serviço – o grande trade-off presente na gestão. Esse trade-off tem se tornado cada vez mais representativo, já que os custos com estoque se tornam a cada dia mais representativos no cenário brasileiro, como revela a Pesquisa de Custos Logísticos.
Em 2002, foi atribuído grau 3,6 na priorização na redução de custos com estoque – onde 5 representa o valor mais alto. Em 2009, esse valor se aproxima de 4,3, revelando a importância da gestão dos estoques.
Bibliografia
CASELLA, G.; BERGER, R. L. Statistical Inference.
2nd ed. Pacific Grove. Duxbury, 2002. 660 p.
DA SILVA, G. L. C. Modelo de Estoque para Peças de Reposição Sujeitas à Demanda Intermitente e Lead Time Estocástico. 2009. 75 f. Dissertação (Mestrado em Engenharia de Produção) – Escola de Engenharia, Universidade Federal de Minas Gerais, Belo Horizonte.
SILVER, E. A.; PYKR, D. F.; PETERSON, R. Inventory Management and Production Planning and Scheduling.
3nd ed. John Wiley & Sons, 1998. 754 p.
WANKE, P. Gestão de Estoques na Cadeia de Suprimentos.1ª ed. São Paulo. Editora Atlas. 2003. 176 p.
WARD, J. B. Determining Reorder Points When Demand is Lumpy. Management Science, v. 24, n.6, pp.
623-632, 1978.
WANKE, P. Gestão de Peças de Reposição de Baixíssimo Giro. 2002. Disponível em: http://www.ilos.com.
br/site/index.php?option=com_content&task=view&id=1 103&Itemid=74
WANKE, P. Gestão de Peças de Reposição de Baixo Giro. 2003. Disponível em: https://ilos.com.br/ site/index.php?option=com_content&task=view&id=767
&Itemid=74
YEH, Q. J.; CHANG, T. P.; CHANG, H. C. An Inventory Control Model With Gamma Distribution. Microelectron.
Reliab., v. 37, n. 8, pp. 1197-1201, 1997.
1 – A primeira parte do artigo foi publicada na edição de novembro (nº 180) da Tecnologística 2 – Pesquisa do Instituto ILOS – Custos Logísticos no Brasil 2010 3 – Para maiores informações sobre o uso da distribuição Stuttering Poisson, ver Ward, J. B.
Determining Reorder Points When Demand is Lumpy.
Management Science, v.24, n.6, p. 623-632, 1978