As últimas três décadas foram marcadas por fortes transformações nas relações de fornecimento entre indústria e varejo. São diversos os relatos sobre essas diferentes relações de fornecimento (Christopher, 2000). Diversas indústrias reestruturaram suas redes de distribuição para atender à contínua demanda do varejo por menores estoques e maiores níveis de serviço (Hoek, 1998a e 1998b). As iniciativas gerenciais que culminaram com a reestruturação dessas operações atendem por diferentes denominações: Efficient Consumer Response – ECR, Quick Response – QR (Fiorito e May, 1995), Vendor Managed Inventory – VMI (Waller e Johnson, 1999), Continuous Replenishment – CR (Ellinger e Taylor, 1999) e Continuous Replenishment Program – CRP (Liz, 1999 e Andraski, 1994).
Em linhas gerais, essas iniciativas baseiam-se num objetivo comum: reduzir a dependência de previsões de venda na indústria e os níveis de estoque no varejo, com simultâneo aumento nos níveis de serviço (Lee e Padmanabhan, 1997). Segundo Vergin e Barr (1999), a cooperação e o compartilhamento de informações da demanda do consumidor final permitiriam esse objetivo (Kiely, 1998). No entanto, a literatura não é conclusiva com relação à homogeneidade dos resultados alcançados sob os prismas da indústria e do varejo. Enquanto no varejo a reestruturação das operações na indústria permitiu a redução dos estoques, na indústria houve casos de redução e de aumento dos mesmos (Harrison e Voss, 1990 e Romero, 1991).
É possível que os benefícios “prometidos” por essas iniciativas com relação aos níveis de estoque (e também aos custos totais) na indústria dependam da aderência entre o posicionamento estratégico de sua rede de distribuição, as características do produto e da demanda e o que se espera dos indicadores de desempenho no varejo (Johnson e Stice, 1993 e Jones, 1991).
Wanke e Zinn (2004) fornecem um exemplo nesse sentido a partir da iniciativa de VMI, que pode ser utilizada para ilustrar a escolha entre centralização e descentralização da distribuição sob diferentes trade-offs entre giro dos estoques na indústria e tempo de entrega exigido pelo varejo. No VMI, o estoque da indústria pode ser localizado num centro de distribuição avançado e a entrega para o varejo ser praticamente instantânea.
A questão-chave é como a indústria deve ressuprir o estoque no varejo. As escolhas são um estoque centralizado na indústria combinado com um tempo de entrega mais longo para o varejo (e menor giro) ou um estoque descentralizado, próximo ao varejo, com entregas mais rápidas (e maior giro). Em essência, o que se está buscando é responder se essa iniciativa gerencial (VMI) deveria ser estruturada via distribuição direta (estoque centralizado na indústria ou num centro de distribuição único) ou via distribuição escalonada (estoque descentralizado num centro de distribuição local). Qual o tipo de distribuição mais adequado?
De modo qualitativo, o impacto do tipo de distribuição nos principais indicadores de desempenho na indústria e no varejo é relativamente bem documentado e são diversas as evidências empíricas sobre o sentido dos efeitos principais da distribuição direta e da distribuição escalonada (Evers, 1999; Leew e Goor, 1999; Evers e Beier, 1998; Tallon, 1993; Amstel e Amstel, 1985).
Alguns desses impactos já foram citados em livros há mais de vinte anos. Por exemplo, Bowersox et al. (1980) afirmam que a distribuição escalonada implica maiores níveis de estoque para a indústria, sendo preferível quando os produtos são de baixo custo adicionado e existe a possibilidade de consolidar o transporte entre a indústria e o centro de distribuição (Jayaraman, 1998 e Carter e Ferrin, 1996). A distribuição direta a partir da indústria tende a se verificar com produtos de alto custo adicionado, sobretudo se os volumes são elevados e há proximidade com o varejo (Bowersox e Closs, 1996). O alto custo adicionado também pode inibir intermediários interessados em manter estoques, levando a indústria à distribuição direta ao consumidor final (Lambert e Stock, 1998).
De acordo com Levy e Weitz (1998), a escolha do tipo de distribuição pelo varejo deve considerar simultaneamente o custo total associado a cada alternativa e o atendimento ao cliente, ou seja, ter o produto na loja quando o consumidor final quiser comprá-lo. A distribuição escalonada permite que o varejo opere com menos estoque, resultado de entregas mais freqüentes a partir do centro de distribuição. Além disso, um melhor balanceamento entre sobras e faltas pode decorrer da revisão, sempre que necessário, das quantidades solicitadas ao centro de distribuição (Berman e Evans, 1998).
A distribuição direta, pelo fato de consumir tempo no varejo com o recebimento e o processamento de pedidos, pode levar a ressuprimentos menos freqüentes e à consolidação dos envios. Segundo Levy e Weitz (1998), a distribuição direta no varejo também é favorecida pela proximidade geográfica.
Percebe-se que, sob os prismas da indústria e do varejo, a escolha do tipo de distribuição é indiferente quando são considerados os critérios distância entre a origem e o destino e volume de compras: maiores distâncias e menores volumes, distribuição escalonada com consolidação via centro de distribuição; menores distâncias e maiores volumes, distribuição direta da indústria ao varejo. Quando o critério de análise é o nível de estoque na indústria e no varejo, a distribuição escalonada implica maiores níveis de estoque para o primeiro e menores para o segundo e a distribuição direta, vice-versa.
A REDE EM ANÁLISE
A questão que se coloca agora é, considerando-se o prisma da indústria, sob quais condições a distribuição direta e a distribuição escalonada poderiam ser utilizadas de modo complementar, e não excludente, para o atendimento aos mercados e em quais proporções. Mais especificamente, deseja-se responder como essas proporções poderiam ser ajustadas para minimizar os custos totais a partir de um maior equilíbrio entre os níveis de estoque de segurança (maiores na distribuição escalonada) e os gastos com transporte (maiores na distribuição direta). Qual o ferramental (metodologias, modelos e sistemas) disponível para auxiliar a indústria avaliar essa decisão?
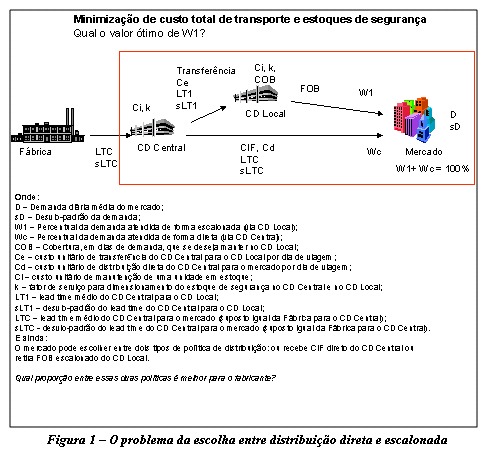
A resposta para essas questões vai tomar como ponto de partida uma rede simples, composta por uma fábrica, um CD Central, um CD Local e um universo de clientes a serem atendidos (mercado). A esses clientes é oferecida uma política de distribuição bastante comum em empresas brasileiras: receber CIF diretamente do CD Central com um lead time maior ou retirar FOB do CD Local com um lead time menor. Para a indústria, essa política de distribuição se resume a: gastar mais com transporte na distribuição direta CD Central-Mercado e economizar nos estoques de segurança; ou gastar menos na distribuição escalonada, apenas com a transferência do CD Central para o CD Local, e imobilizar capital em estoques de segurança no CD Local.
Na figura 1 é ilustrada não apenas essa rede logística simples, mas também são apresentadas as principais variáveis envolvidas na decisão de determinar a proporção ótima entre distribuição direta (Wc) e distribuição escalonada (W1). Deve ser ressaltado que W1 e Wc devem somar 100%.
 |
METODOLOGIAS ALTERNATIVAS PARA RESOLVER O PROBLEMA
Existem duas abordagens para tentar resolver esse problema. A mais clássica e conhecida é associada às técnicas de programação matemática no campo da pesquisa operacional, enfatizando os custos de transporte e de instalação e relegando ao segundo plano os custos de estoques. Trabalhos mais recentes como os de Jayaraman (1998) e Croxton e Zinn (2005)* têm tentado estabelecer pontes entre os modelos de programação matemática e os níveis de estoque, ainda que desconsiderando a correlação da demanda entre os ramos ou pernas da rede logística.
A menos difundida, porém adequada para redimensionar redes logísticas já existentes, é derivada das diferentes maneiras de se calcular o efeito portfólio, ou seja, o percentual esperado de redução de estoques de segurança a partir da centralização do atendimento. Nessa abordagem, os custos de transporte são relegados ao segundo plano e predominam as análises de como os coeficientes de correlação entre as diferentes pernas da rede logística podem contribuir na consolidação dos estoques de segurança numa menor quantidade de instalações. Mahmoud (1992) tentou estabelecer uma ponte entre a redução dos estoques de segurança e o impacto em outros componentes do sistema logístico como, por exemplo, os custos totais.
Essa descrição não pretende esgotar todas as particularidades dessas duas metodologias alternativas, mas chamar atenção para que elas podem indicar resultados conflitantes, mesmo quando é considerada uma rede relativamente simples como aquela apresentada na Figura 1.
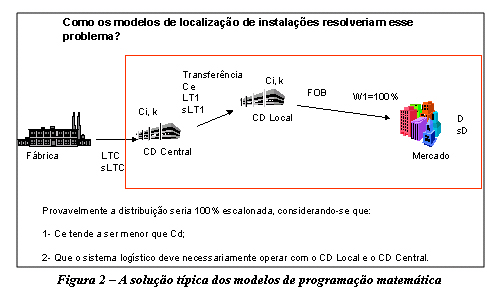
Por exemplo, na Figura 2 é ilustrado o padrão típico de solução para os modelos de programação matemática quando se considera que CD Central e CD Local devem permanecer abertos e que necessariamente o custo de transporte via CD Local (parte do trajeto é FOB) é menor que o custo de transporte a partir do CD Central (CIF). Toda a distribuição deveria ser feita pelo CD Local (W1 = 100%) e não haveria espaço para a distribuição direta. Mas a que custo de manutenção de estoques de segurança em ambos os CDs?
 |
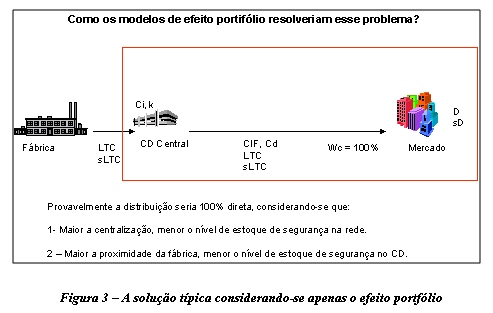
Já na Figura 3 é apresentado o típico padrão de decisão quando se analisa o problema sob o prisma do efeito portfólio. A duplicidade de estoques de segurança em ambos os CDs é o X da questão, o que levaria à consolidação dos estoques de segurança no CD mais próximo da fonte de suprimento, ou seja, levaria à centralização dos estoques no CD Central que está mais próximo da fábrica. Em outras palavras, W1 = 0% e conseqüentemente Wc = 100%. Mas a que nível de gastos com transporte?
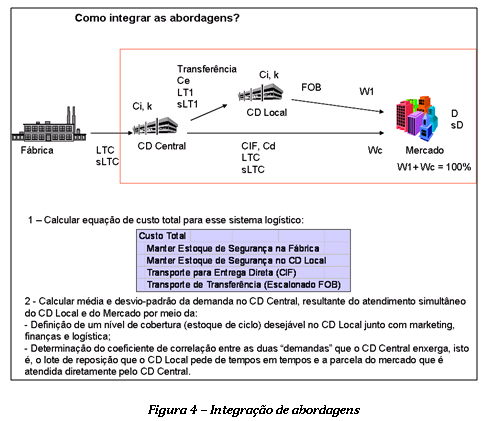
Como é ilustrado na Figura 4, percebe-se a necessidade de se integrar ambas as abordagens para que sejam obtidas respostas mais satisfatórias em termos do planejamento da distribuição. Nem apenas distribuição direta, nem apenas distribuição escalonada, mas um mix entre esses dois tipos. Diversos pesquisadores em universidades e empresas de consultoria vêm trabalhando continuamente para uma maior integração dessas abordagens em uma única metodologia, o que, se alcançado, pode gerar benefícios significativos em termos de economia de recursos humanos e materiais despendidos nessas questões, implicando também significativa evolução no modo como as redes de distribuição são planejadas hoje em dia.
 |
Na Figura 4 são apresentados alguns dos elementos necessários para viabilizar essa integração, ainda que aplicados na rede simples da qual trata esse artigo. São eles: (a) a determinação da equação de custo total que contém o principal trade-off da análise (no caso, os gastos com transportes versus os níveis de estoque de segurança na rede) e (b) a determinação de como se comporta o coeficiente de correlação entre as demandas do CD Local e do mercado para CD Central.
A demanda do CD Local para o CD Central depende, dentre outras variáveis, da cobertura de estoque de ciclo (COB), em termos de dias de consumo, que a área comercial ou de marketing acha razoável manter no CD Local. De tempos em tempos essa cobertura é consumida pelo atendimento ao mercado e a necessidade um lote de reposição, proporcional a essa cobertura, é gerada para o CD Central.
 |
Na seção seguinte é apresentado o resultado analítico para esse problema, ou seja, a fórmula para determinar o valor ótimo de W1, além de análises de sensibilidade com os principais parâmetros para tomada de decisão. Antes de prosseguirmos, ressaltamos as principais premissas adotadas para derivar esse resultado: o CD Central está eqüidistante da fábrica e do mercado, os estoques de segurança são determinados pelo fator de serviço k da distribuição normal e os pedidos são colocados eletronicamente do CD Local para o CD Central, gerando custos fixos desprezíveis relacionados ao ressuprimento do lote. Além disso, a cobertura no CD Local é uma variável de mercado a ser definida pela área comercial.
PRINCIPAIS RESULTADOS
Na Figura 5 é apresentada a fórmula para o percentual ótimo de distribuição escalonada, dada a rede simples apresentada na Figura 1 e as premissas indicadas anteriormente. As barras ao redor da fórmula de W1 Ótimo indicam que está sendo considerado o módulo da expressão e deve ser lembrado que não existem soluções reais (raiz negativa) quando –a2*a42+a12< 0.
 |
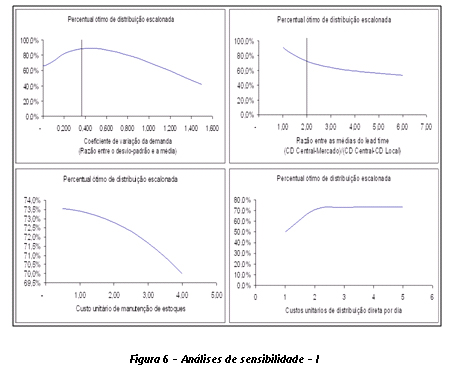
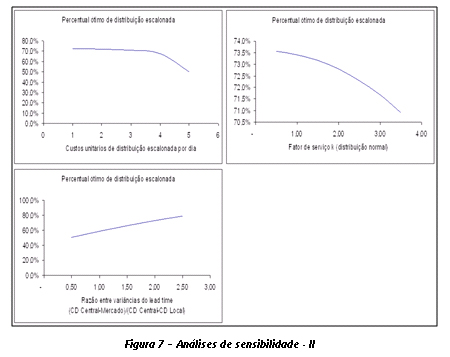
As Figuras 6 e 7 apresentam análises de sensibilidade para as principais variáveis do problema, considerando um conjunto de dados reais, com a cobertura do CD Local definida pela área comercial. A seguir, uma breve discussão sobre o impacto de cada uma dessas variáveis no percentual ótimo de distribuição escalonada (W1 ótimo).
- Coeficiente de variação da demanda (CVd). Conforme ilustrado na Figura 6, o coeficiente de variação da demanda apresenta o trade-off “mais interessante” com relação ao percentual ótimo de distribuição escalonada. Quanto maior este coeficiente, ou seja, quanto maior a incerteza da demanda, menor o percentual de distribuição escalonada e maior o percentual de distribuição direta. Só que isso acontece a partir de determinado ponto. Valores pequenos do coeficiente de variação da demanda (até 0,5) favorecem a distribuição escalonada. Esses valores indicam até que ponto vale a pena manter estoques de segurança numa instalação intermediária para economizar os gastos de transporte com a entrega direta.
- Custo unitário de manutenção de estoques (Ci). Como não poderia deixar de ser, quanto maiores os custos de manutenção de estoques, menor a propensão para a distribuição escalonada.
- Custos unitários de distribuição direta por dia (Cd) e custos unitários de distribuição escalonada por dia (Ce). Assim como o trade-off anterior, esses também são “fáceis” de interpretar. Maiores os custos de distribuição direta, maior o percentual de distribuição escalonada. Por outro lado, maiores os custos de distribuição escalonada, menor o percentual de distribuição escalonada.
- Razão entre variâncias do lead-time (y). Quanto maior for a incerteza do CD Central no atendimento ao mercado comparativamente ao seu atendimento ao CD Local, maior deve ser o percentual de distribuição escalonada, pois os estoques de segurança necessários para assegurar determinado nível de serviço serão proporcionalmente menores no CD Local do que no CD Central.
- Razão entre as médias do lead-time (x). Quanto mais próximo do CD Central for o CD Local e quanto mais distante do mercado forem ambos os CDs, o CD Local vai perdendo importância como elemento para minimização dos custos totais e, conseqüentemente, menor o percentual de distribuição escalonada. Um dado curioso é que em situações extremas e mantendo todo o resto constante, os valores de W1 e Wc convergem, respectivamente, para 40% e 60%, ou seja, 40% para entrega FOB via CD Local e 60% para entrega direta a partir do CD Central. Em outras palavras, para CDs Locais que são “satélites” de um CD Central afastado do mercado, seria verificado um piso ótimo de aproximadamente 40% para os dados analisados.
- Fator de serviço (k). Quanto maior o nível de serviço desejado em termos de disponibilidade de produto, menor o percentual de distribuição escalonada, basicamente em função de dois motivos: (a) os estoques de segurança começam a ficar excessivos na rede de distribuição em relação aos gastos com transporte e (b), do ponto de vista de nível de serviço, o papel de um CD Local é contribuir, sobretudo, com a dimensão de prazo de entrega, e não com a dimensão de disponibilidade de produto (a qual depende do fator k).
 |
 |
CONCLUSÃO
Em resumo, os resultados mostram que a coexistência de distribuição direta com distribuição escalonada pode ser a melhor política a ser adotada pelas indústrias na maioria das vezes. Duas variáveis merecem destaque: o coeficiente de variação da demanda e a proximidade entre o CD Local e o CD Central relativamente ao afastamento do CD Central do mercado. Com relação à primeira variável, estabelece-se um “divisor de águas” sobre o que seria uma incerteza da demanda alta ou baixa: para valores do coeficiente de variação da demanda ao redor de 0,5 o percentual ótimo de distribuição escalonada deixa de aumentar (CVd < 0,5) e passa a diminuir sistematicamente (CVd > 0,5). Já com relação à segunda variável, o percentual de distribuição escalonada é fortemente influenciado se o CD Local é uma instalação satélite ao CD Central ou ao mercado, sendo esse percentual tão maior quanto mais próximo for do mercado o CD Local.
Nesse artigo, foi discutida a importância de se desenvolverem novas abordagens para o planejamento do tipo de distribuição, se direta ou escalonada e qual o percentual ótimo de ambas. Para tanto, foi considerada a perspectiva de custos da indústria e uma rede de distribuição simples em que diversas variáveis foram consideradas simultaneamente. A solução analítica para o percentual ótimo de distribuição escalonada foi determinada e diversas análises de sensibilidade foram conduzidas, com o objetivo de evidenciar a importância relativa das principais variáveis do problema e entender os trade-offs envolvidos na tomada de decisão.
BIBLIOGRAFIA
AMSTEL, M.; AMSTEL, W.. 1985, “Economic Trade-offs in Physical Distribution”, Intl. Journal of Physical Distribution & Materials Management, v. 17, n.7, pp.15-54.
ANDRASKI, J.. 1994, “Foundations for Successful Continuous Replenishment Programs”, Intl. Journal of Logistics Management, v. 5, n. 1, pp. 1-8.
BERMAN, B.; EVANS, J.. 1998, Retail Management: A Strategic Approach. Prentice Hall.
BOWERSOX, D.J.; COOPER, M.; LAMBERT, D.; TAYLOR, D.. 1980, Management in Marketing Channels. 1 ed., New York, McGraw-Hill.
BOWERSOX, D.J.; CLOSS, D.J.. 1996, Logistical Management – The Integrated Supply Chain Process, 1 ed., McGraw-Hill.
CARTER, J.R.; FERRIN, B.G.. 1996, “Transportation Costs and Inventory Management: Why Transportation Cost Matter”, P& IM Journal, Third Quarter, pp. 58-62.
CHRISTOPHER, M.. 2000, “The Agile Supply Chain – Competing in Volatile Markets”, Industrial Marketing Management, v. 29, n. 1, pp. 37-44.
CROXTON, K.L.; ZINN, W.. 2005, “Inventory considerations in network design”. Journal of Business Logistics, v. 26, n. 1, pp.149-168.
ELLINGER, A.; TAYLOR, J.. 1999, “Automatic Replenishment Programs and Level of Involvement: Performance Implications”, Intl. Journal of Logistics Management, pp. 25-36.
EVERS, P.T.; BEIER, F.J.. 1998, “Operational Aspects of Inventory Consolidation Decision Making”, Journal of Business Logistics, v. 19, n. 1, pp. 173-189.
EVERS, P.T.. 1999, “The Effect of Lead Times on Safety Stocks”, P&IM Journal, Second Quarter, v. 40, n. 2, pp. 6-10.
FIORITO, S.S.; MAY, E.G.. 1995, “Quick Response in Retailing”, Intl. Journal of Retail and Distribution Management, v. 23, n. 5, pp. 12-21.
HARRISON, A.; VOSS, C.. 1990, “Issues in setting up JIT supply”, Intl. Journal of Operations and Production Management, v. 10, n. 2, pp. 84-93.
HOEK, R.I.. 1998a, “Logistics and Virtual Integration”, Intl. Journal of Physical Distribution & Logistics Management, v. 28, n. 7, pp. 508-523.
HOEK, R.I.. 1998b, “Reconfiguring the Supply Chain to Implement Postponed Manufacturing”, Intl. Journal of Logistics Management, v. 9, n. 1, pp. 95-110.
JAYARAMAN, V.. 1998, “Transportation, Facility Location and Inventory Issues in Distribution Network Design”, Intl. Journal of Operations & Production Management, v. 18, n. 5, pp. 471-494.
JOHNSON, G.H.; STICE, J.D.. 1993, “Not Quite Just-in-Time Inventories”, The National Public Accountant, v. 38, n. 3, pp. 26-29.
JONES, D.J., 1991, “JIT and EOQ Model: Odd Couple No More”, Management Accounting, v. 72, n. 8, pp. 54 –57.
KIELY, D.A.. 1998, “Synchronizing Supply Chain Operations with Consumer Demand Using Customer Data”, The Journal of Business Forecasting Methods & Systems, Winter, pp.3-9.
LAMBERT, D.M.; STOCK, J.R.; ELLRAM, L.M.. 1998, Fundamentals of Logistics Management. 1 ed., New York, Irwin-McGraw Hill.
LEE, H.L.; PADMANABHAN, V.. 1997, “The Bullwhip Effect in Supply Chains”, Sloan Management Review, Spring, pp. 93-102.
LEEUW, S.D.; GOOR, A.R.. 1999, “The Selection of Distribution Control Techniques”, The Intl. Journal of Logistics Management, v. 10, n. 1, pp. 97-112.
LEVY, M.; WEITZ, B.. 1998, Retailing Management. 3 ed., New York, McGraw Hill.
LIZ, P.. 1999, “CRP Investment Pays Off in Many Ways”, Drug Store News, v. 21, n. 2, p.26.
MAHMOUD, M.M.. 1992, “Optimal inventory consolidation schemes: a portfolio effects analysis”. Journal of Business Logistics, v. 13, n. 1, pp.193-214.
ROMERO, B.. 1991, “The Other Side of Supply Management”, P&IM Journal, v. 32, n. 4, pp. 1-3.
TALLON, W.. 1993, “The Impact of Inventory Centralization on Aggregate Safety Stock”, Journal of Business Logistics, v. 14, n. 1, pp. 185-196.
VERGIN, R; BARR, K.. 1999, “Building Competitiveness in the Grocery Supply Chain Through Continuous Replenishment Planning”, Industrial Marketing Management, v. 28, pp. 145-153.
WALLER, M.; JOHNSON, M.. 1999, “Vendor Managed Inventory in the Retail Supply Chain”, Journal of Business Logistics, v.20, n.1, pp. 183-198.
WANKE, P.; ZINN, W.. 2004, “Strategic Logistics Decision Making”, Intl. Journal of Physical Distribution and Logistics Management, v. 34, n. 6, pp. 466-478.
*Veja artigo de Walter Zinn e Keely Croxton “Considerações sobre o estoque no desenho de redes logísticas”, 1ª e 2ª partes, nas edições 133 (dezembro de 2006) e 134 (janeiro de 2007) da Tecnologística – já disponível também no site: www.tecnologistica.com.br/site/lista_anteriores.asp