Capacidade é “o volume de saída que um sistema é capaz de atingir em um período específico de tempo” (Yang, 2001). Ao se falar de capacidade, provavelmente a primeira coisa em que se pensa seja capacidade produtiva. No entanto, capacidade é um termo muito mais amplo e abrangente. Neste artigo, abordaremos o tema com o foco em decisões de capacidade em aplicações logísticas: Quantas rampas de conferência devem ser construídas na ampliação de um centro de distribuição? Que tamanho devem ter os tanques de estocagem de produtos acabados de uma petroquímica para suportar a operação em cinco anos? Que impacto as novas tecnologias podem ter na operação futura? Essas são algumas perguntas que devem ser respondidas para a elaboração de um planejamento estratégico de capacidade.
É importante ressaltar que, muitas vezes, não é dada a devida importância para a questão de capacidade nas empresas. Assim, executivos podem se ver em situações nas quais percebem que investimentos já deveriam ter sido feitos e que não poderão atender à demanda por falta de capacidade.
A criticidade de um planejamento de capacidade aumenta em função do tempo necessário para implementar uma expansão. Se a capacidade de uma operação pode ser ampliada em poucos dias, um plano para os próximos cinco anos pode parecer desnecessário. Porém, caso os projetos exijam meses ou anos para ser executados, um planejamento estratégico de capacidade é indispensável.
Ao decidir o nível de capacidade que deve manter ao longo do tempo, uma organização deve avaliar o trade-off entre a sua falta e o seu excesso. Em um cenário de falta de capacidade, a empresa não atende por completo à demanda, podendo perder clientes pelo nível de serviço deficiente, abrindo espaço para o avanço dos concorrentes. Por outro lado, o excesso de capacidade leva à ociosidade dos recursos, incorrendo em custo de oportunidade, ou a estratégias forçadas para o aumento da demanda, como, por exemplo, a redução de preços.
Dessa forma, encontra-se um problema muito semelhante ao problema da definição de estoques de segurança de produtos. A literatura fornece algumas metodologias para a definição dos chamados colchões de capacidade, que, semelhantemente aos estoques de segurança, têm como objetivo garantir um determinado nível de atendimento, dadas as variabilidades existentes. Hayes e Wheelwright (1984), por exemplo, discorrem sobre uma metodologia para a definição desse colchão de capacidade, que deve refletir a magnitude da relação:
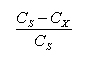 |
Na fórmula, Cs representa o custo da falta (short) e Cx representa o custo do excesso (excess). No entanto, essa abordagem apresenta algumas fragilidades. Definir esses parâmetros de forma acurada é algo de extrema dificuldade, se observarmos que custo do excesso pode, por exemplo, variar em função da quantidade de capacidade a ser instalada; e o custo de falta pode incluir componentes de difícil quantificação como, por exemplo, a margem perdida de vendas futuras por perda de clientes e os danos na imagem e reputação da organização.
Apesar disso, é importante ressaltar que a relação captura o tipo de trade-off existente, podendo ajudar no direcionamento da decisão, mesmo que o valor em si não seja utilizado matematicamente para a definição do colchão. Dependendo deste trade-off, o plano de expansão de capacidade pode ser direcionado por uma das políticas descritas a seguir.
Política A: Evitar falta
Caso o custo da falta seja superior ao custo de excesso, a organização deve tender para uma política de manter um colchão de capacidade relativamente grande e, assim, garantir uma baixa probabilidade de não atendimento da demanda. Nestes casos, deve-se, no extremo, optar pelo comportamento de expansão ilustrado no Gráfico 1.
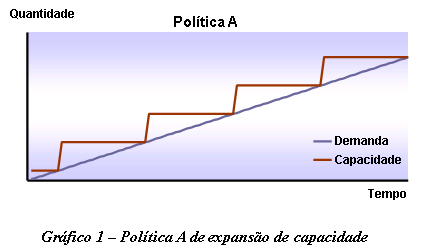 |
A falta de capacidade de armazenagem em um processo de produção contínua, como no setor petroquímico, pode levar à parada da planta. Neste caso, o custo da falta de capacidade é representado pela margem cessante causada pela parada, sendo claramente maior que o custo do excesso.
Política B: Seguir a previsão
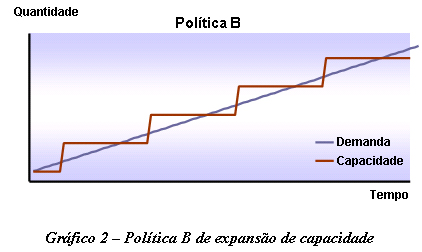
Caso o custo de falta seja semelhante ao custo de excesso, o plano de expansão deve garantir que a probabilidade de ocorrência de falta de capacidade seja parecida com a de ocorrência de excesso. Assim, esta política sugere que a organização tente adequar a capacidade produtiva à previsão de demanda. O Gráfico 2 representa o comportamento da capacidade frente à demanda ao longo do tempo.
 |
Política C: Evitar excesso
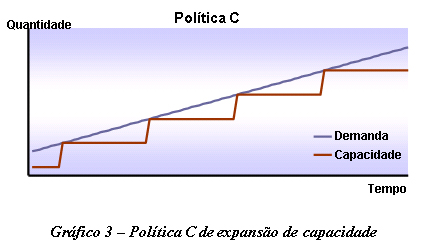
Caso o custo do excesso seja superior ao custo da falta de capacidade, a empresa deve manter um colchão “negativo”, de modo a garantir que a probabilidade de ocorrência de falta seja maior que a probabilidade do excesso. Essa política leva a uma alta taxa de utilização dos recursos, gerando, por conseqüência, um maior retorno sobre investimentos que as outras duas já apresentadas. No entanto, deve-se atentar para o fato de que a sua adoção também pode levar a uma deterioração da imagem e do posicionamento da organização no mercado. O comportamento de expansão de capacidade referente a esta política está ilustrado no gráfico 3.
 |
No entanto, é importante frisar que o planejamento estratégico de capacidade deve estar alinhado com a estratégia de negócio da organização. Sendo extremamente difícil calcular exatamente qual o tamanho ideal do colchão de capacidade, a organização deve atentar para outros fatores estratégicos que geram e sofrem conseqüências advindas das decisões de capacidade – quando expandir, quanto expandir – ao definir o planejamento estratégico.
Uma expansão de capacidade pode ser utilizada como ativadora de demanda, fazendo com que esta cresça mais rapidamente quando comparada a um cenário sem expansão, ou como ferramenta para intimidar a concorrência, principalmente os players de menor porte. Por exemplo, um aumento nos recursos de uma empresa, de modo que esta consiga estar presente e levar seus produtos a uma certa região com um preço menor, pode estimular a demanda, o que não aconteceria se tal decisão não tivesse sido tomada.
No entanto, a capacidade de um sistema está diretamente relacionada com a quantidade e características dos recursos disponibilizados. E dificilmente a capacidade total de um sistema pode ser definida apenas por um recurso. Normalmente, é necessário um conjunto de diferentes recursos para compor a capacidade de um sistema. Assim sendo, o Planejamento Estratégico de Capacidade deve definir a quantidade de cada um dos recursos necessários ao longo do tempo a partir das suposições e previsões futuras.
Para isso, o tomador de decisão precisa entender como os recursos estão relacionados, como cada um deles pode impactar nos demais, como a quantidade e eficiência de cada um deles podem alterar a capacidade total e como o sistema reage sob certas condições que não existem hoje, mas podem se tornar realidade no futuro. Ter este embasamento para a tomada de decisão não é nada simples, uma vez que uma estratégia de capacidade é baseada em uma série de suposições e previsões de longo prazo sobre o mercado (demanda), a tecnologia e o comportamento competitivo, sendo as principais:
- A previsão de crescimento e estimativa da variabilidade da demanda;
- Eficiência, disponibilidade e custos de construção e operação dos recursos;
- O comportamento dos demais players e fornecedores.
Obviamente, todas essas previsões e suposições são estritamente necessárias, e por definição trazem consigo um elevado grau de incerteza que precisa ser adequadamente considerado.
AS INCERTEZAS
Lidar com incertezas de uma forma consistente em uma organização não é uma tarefa trivial. Trabalhar com valores únicos e médios neste tipo de ambiente geralmente leva a interpretações falhas e, conseqüentemente, a decisões gerenciais equivocadas. Ao mesmo tempo, considerar essas incertezas em análises e avaliações por meio de estatísticas como percentis, desvio padrão ou covariância também não é algo muito simples. No caso do Planejamento de Capacidade não é diferente. Além da demanda futura, que consiste em um dos principais dados de entrada para um estudo de capacidade, as incertezas também estão presentes em outros parâmetros, como, por exemplo, os tipos de recursos disponíveis, a eficiência desses recursos ou a disponibilidade dos mesmos.
O grau de incerteza presente é diretamente proporcional ao horizonte do planejamento, ou seja, para análises de capacidade de longo prazo, a incerteza contida nas estimativas de demanda futura é maior quando comparada à incerteza referente a previsões de demanda realizadas para alimentar análises de capacidade de curto prazo. Além disso, estimar outros fatores como o comportamento da concorrência e dos fornecedores no longo prazo é uma tarefa de extrema dificuldade.
Incorporar as incertezas presentes, ou pelo menos as principais delas, é muito importante para o planejamento de capacidade de longo prazo, uma vez que pode mudar significativamente a decisão tomada e, conseqüentemente, os investimentos necessários para a implantação do plano de expansão.
Existem alguns métodos que podem ser utilizados em um estudo de análise de capacidade, como modelagem analítica, programação estocástica e simulação. No entanto, a complexidade gerada pelas incertezas presentes em diversas variáveis interdependentes geralmente dificulta seriamente a adoção de uma metodologia analítica ou de programação para a resolução do problema. Assim, será detalhado como a simulação pode ser aplicada em um estudo de análise de capacidade.
INTRODUÇÃO À SIMULAÇÃO E APLICAÇÃO PRÁTICA
Segundo Saliby (1999), “…simulação consiste no processo de construção de um modelo que replica o funcionamento de um sistema real ou idealizado (ainda a ser construído) e na condução de experimentos computacionais com este modelo, com o objetivo de melhor entender o problema em estudo, testar diferentes alternativas para sua operação e assim propor melhores formas de operá-lo.” Essa definição deixa claro como a simulação pode ser utilizada como ferramenta para um estudo de análise de capacidade. O modelo deve representar o sistema ou sub-sistema logístico a ser estudado, considerando os relacionamentos existentes entre recursos e atividades, ficando próximo o suficiente da operação real, de modo a garantir resultados robustos e confiáveis.
Para atingir esse objetivo, é altamente recomendável seguir a metodologia diagramada na Figura 1.
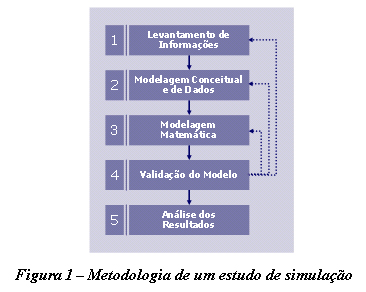 |
Etapa 1: Levantamento de informações
Nesta etapa, o analista de simulação deve obter todas as informações necessárias para o entendimento claro do sistema a ser modelado e dos objetivos que devem ser alcançados. É importante definir claramente o escopo e ter em mente quais perguntas precisam ser respondidas pelo modelo.
Etapa 2: Modelagem conceitual e de dados
Na modelagem de dados, após a coleta, estes precisam ser tratados de modo a identificar possíveis falhas e inconsistências que podem ter impacto na qualidade do resultado final – vale a máxima garbage in, garbage out. Após o tratamento, os dados devem ser utilizados de forma a definir as distribuições de probabilidade que representarão as incertezas e outros fenômenos aleatórios no modelo.
Além disso, nesta etapa também é realizada a modelagem conceitual, que consiste na definição da lógica do modelo e na sua representação para que todas as pessoas envolvidas no processo possam entendê-lo. É nesta etapa que, por exemplo, definem-se prioridades de atendimento, fluxo de materiais, recursos envolvidos e seus relacionamentos com as atividades, entre outros. Pode-se dizer que se trata da etapa mais importante do desenvolvimento de um modelo de simulação.
Etapa 3: Modelagem matemática
Nela, o modelo conceitual é convertido em um modelo computacional por meio da utilização de alguma linguagem de programação ou de algum software de simulação. É importante ressaltar que os softwares de simulação atuais permitem um alto nível de customização, utilizando interface gráfica e levando à redução do tempo de implementação do modelo. Dessa forma, dificilmente um analista de simulação precisará recorrer a uma linguagem específica de programação.
Etapa 4: Validação do modelo
Após a construção do modelo matemático computacional, este precisa ser comparado ao modelo conceitual de modo a avaliar se a lógica definida anteriormente foi fielmente implementada. Em seguida, deve-se rodar o modelo e gerar alguns resultados com o objetivo de verificar se este consiste numa representação precisa da realidade. Geralmente, isso é feito inserindo dados históricos de um determinado período e comparando o resultado do modelo com o que realmente aconteceu na operação neste período.
É importante comentar que, dependendo dos resultados obtidos, pode-se identificar a necessidade de retornar a etapas anteriores. Isso porque o modelo pode retornar resultados equivocados devido a problemas de entendimento do sistema, na modelagem conceitual, nos dados de entrada ou na implementação computacional.
Etapa 5: Análise dos resultados
Somente depois de validado pode-se utilizar o modelo para a realização dos experimentos. Nesta etapa, são realizadas diversas rodadas em função dos cenários e variações que se deseja avaliar. É importante ressaltar que a simulação por si só não responde qual seria a melhor alternativa, e sim como um sistema se comporta dada uma certa configuração. Pode-se dizer que a simulação é uma técnica what-if?, ou seja, “o que acontece se…” e não uma técnica que retorna um resultado ótimo, como a otimização. Assim, o plano de experimentos de um modelo de análise de capacidade deve ser elaborado para estudar diversos cenários de demanda, avaliar o impacto de mudanças na concorrência ou nos fornecedores, e, principalmente, verificar diferentes configurações de recursos.
Depois de construído, um modelo de simulação deve apresentar a seguinte estrutura:
- Parâmetros de entrada
- Lógica matemática
- Dados de saída
Tomemos como exemplo o modelo desenvolvido pela Braskem – UNIB em conjunto com o CEL – Centro de Estudos em Logística, e apresentado no XII Fórum Internacional de Logística (2006) para apoiar a elaboração de seu Planejamento Estratégico de Capacidade. Tal modelo abrange vários subsistemas de diversos produtos acabados, o subsistema de matéria-prima e a relação desses subsistemas com portos. A Figura 2 ilustra esses subsistemas e seus relacionamentos.
 |
Dada a complexidade do modelo completo, tomemos apenas um subsistema, o do Produto Z, representado pela Figura 3.
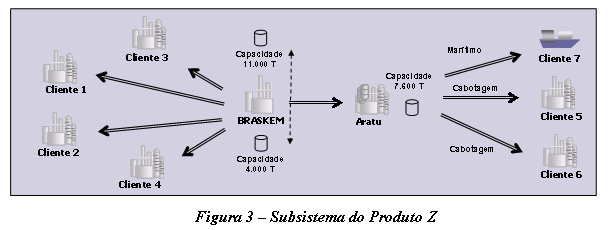 |
O subsistema ilustrado apresenta quatro grupos de entidades. O primeiro é composto pelos clientes do mercado interno que são atendidos diretamente da planta através de dutos. O segundo grupo consiste na planta da Braskem, responsável pela produção e estocagem do produto acabado. O terceiro representa o porto de Aratu, que é ligado à planta por dutovia e é utilizado para atracação e carregamento dos navios que abastecem o mercado externo e outros clientes do mercado interno via cabotagem.
A operação neste subsistema depende de um certo conjunto de recursos. Na planta existem dois tanques de armazenagem, necessários porque, naturalmente, não há sincronismo entre a produção contínua e a demanda. Os dutos são recursos de grande importância, por definirem qual a capacidade de abastecimento dos clientes 1, 2, 3 e 4 e de transferência para o porto de Aratu. O tanque do porto tem o papel de estocar o produto enquanto os navios são aguardados. Por último, os berços do porto restringem o número máximo de navios que podem ser atracados e carregados ao mesmo tempo.
Todos os recursos necessitam ser parametrizados no modelo. Os dutos devem ter suas capacidades inseridas. Os tanques da planta e do porto também devem ter suas capacidades de armazenagem definidas. Certamente, o número de berços também deve ser acrescentado. Além destes, outros parâmetros de entradas são necessários: a demanda de cada um dos clientes atendidos por dutovia; a taxa de produção da planta; a freqüência de chegada das embarcações e a taxa de carregamento das mesmas.
Alguns destes parâmetros foram modelados de forma determinística (valores únicos), como as capacidades de bombeio nos dutos, as capacidades de armazenagem nos tanques, a taxa de produção e o número de berços. Outros, por apresentarem variabilidades e incertezas, foram modelados utilizando distribuições de probabilidades, como a chegada de navios e a demanda dos clientes atendidos por dutovia.
A lógica matemática do modelo deve representar a lógica de fluxos e decisões da operação real. Essa lógica está representada pelo diagrama da Figura 4.
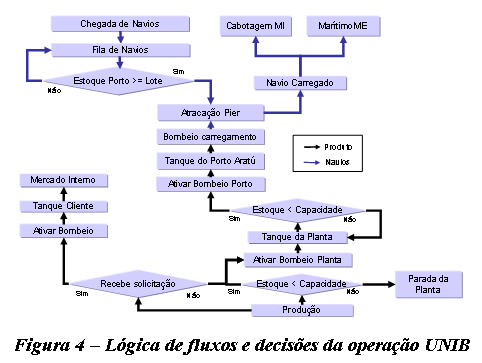 |
Conforme o diagrama sugere, pode-se considerar dois fluxos: o de navios e o de produtos. O fluxo de navios se inicia com a chegada das embarcações e o seu encaminhamento para a fila de atracação. A atracação se dá sob duas condições: disponibilidade de berço e de produto no tanque do porto. Atracado, o navio então é carregado e segue para o seu destino.
O fluxo de produto tem início na produção. Caso haja solicitação de envio para os clientes atendidos por dutovia, o bombeio é ativado e o produto é transferido para os tanques dos clientes. Caso contrário, verifica-se se há espaço para armazenagem no tanque da planta. Caso positivo, o produto é bombeado para este tanque. Se o tanque já estiver com sua capacidade 100% tomada, ocorre a parada da planta. O tanque do porto é ressuprido sempre que tenha capacidade e haja produto no tanque da planta.
Os principais dados de saída do modelo de análise de capacidade são aqueles referentes à utilização dos recursos e ao nível de serviço. No modelo exemplificado, para avaliar a utilização dos recursos foram utilizadas três estatísticas: utilização média, percentil 90 da utilização e percentual do tempo que a utilização ficou acima de 90%. A análise conjunta destas estatísticas permite concluir se um determinado recurso está sub ou super dimensionado.
Conforme mencionado anteriormente, a simulação não retorna um resultado ótimo e sim como o sistema se comporta dadas determinadas condições. Concluir que um recurso está mal dimensionado leva a uma próxima rodada do modelo, alterando os parâmetros deste recurso e analisando novamente os dados de saída. O Quadro 1 mostra alguns resultados de uma rodada do modelo.
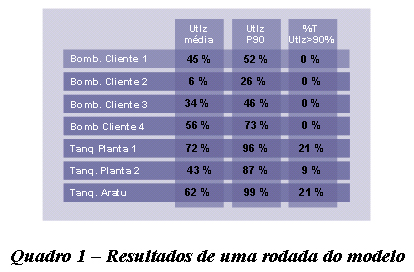 |
Pode-se constatar, por exemplo, que o Tanque 1 da planta parece estar sub-dimensionado, pois, apesar de apresentar uma utilização média de 72%, o percentil 90 chega a 96% e em um quinto do tempo o nível do tanque está acima de 90% da capacidade. Nesta operação, tanques sub-dimensionados podem levar à necessidade de parada da planta e, conseqüentemente, a custos proibitivos. Esta situação ilustra bem o caso no qual o custo de falta de capacidade é maior que o custo de excesso de capacidade. Para avaliar qual será a capacidade adequada do tanque, deve-se rodar novamente o modelo algumas vezes, com diferentes valores de capacidade do tanque 1, maiores que o primeiro valor.
Além dos dados de utilização dos recursos como tanques e dutos, o estudo da utilização dos berços do porto também era de extrema importância. A disponibilidade de berços impacta diretamente na fila de embarcações no porto. Maiores filas levam a maiores tempos de atendimento e a maiores custos de demurrage (multa por atraso na atracação e liberação do navio). Assim, o modelo também foi elaborado para retornar como dados referentes à utilização do porto e à fila de navios.
Construído considerando as principais incertezas, variabilidades e interdependências da operação atual e futura, o modelo desenvolvido pela Braskem-UNIB em conjunto com o CEL permitiu o estudo de diversos cenários e o dimensionamento dos principais recursos logísticos envolvidos. Dessa forma, o Planejamento Estratégico de Capacidade foi elaborado para um horizonte de dez anos, definindo as ações a serem tomadas no tempo, assim como os investimentos necessários.
CONCLUSÃO
O processo de elaboração de um Planejamento Estratégico de Capacidade traz diversos desafios para as organizações. Um dos maiores consiste em como tratar as incertezas originadas pelas previsões e estimativas necessárias para o planejamento. O tratamento adequado destas incertezas é de extrema relevância para garantir a qualidade das decisões tomadas.
Este artigo mostra como a simulação computacional pode ser utilizada como ferramenta em um estudo de análise de capacidade. Um modelo de simulação permite que determinadas ações possam ser testadas e seus efeitos analisados sem que realmente sejam tomadas na realidade.
Apesar de o processo de construção de um modelo matemático não ser uma tarefa simples, necessitando profissionais capacitados e envolvimento de várias pessoas dentro da organização, certamente se paga pela riqueza das análises que podem ser realizadas e pelo embasamento e segurança das conclusões que alimentarão o planejamento estratégico de capacidade da empresa.
BIBLIOGRAFIA
HAYES, ROBERT H.; WHEELWRIGHT, STEVEN C. Restoring Our Competitive Edge – Competing Through Manufacturing. John Wiley & Sons, 1984.
CHWIF, LEONARDO; MEDINA, AFONSO C. Modelagem e Simulação de Eventos Discretos. Bravarte, 2006.
MIEGHEM, JAN A. VAN. Capacity Management, Investment and Hedging: Review and recent Developments. Manufacturing & Service Operations Management, Fall, 2003.
MIRHASSANI, S.A.; LUCAS, C.; MITRA G.; MESSINA, E.; POOJARI, C.A. Computational Solution of Capacity Planning Models Under Uncertainty. Parallel Computing, 2006.
YANG, Y. HELIO; HADDAD, KAMAL; CHOW, CHEE W. Capacity Planning Using Monte Carlo Simulation: An Illustrative Application of Commonly Available PC Software. Managerial Finance, 2001.
COTIAS, ALMIR; NAZARIO, PAULO. Planejamento Estratégico de Capacidade: Braskem UN Insumos Básicos. XII Fórum Internacional de Logística, Agosto 2006.